为了更好地理解细胞存活曲线的放射生物学意义，通常选择合适的生物物理数学模型拟合分析实验数据，并求出表示其特性的放射生物学参数如Do、N、Dq、a和B值。常用的哺乳动物细胞存活曲线有3种类型，即简单的多靶单击模型、带初斜率的多靶单击模型和线性平方模型。

6.5.1.4.1简单的多靶单击模型

        简单的多靶单击模型可用下式表示：

        S=1-(1-e-D/Do)N

        式中S为受到剂量D照射的存活分数；e为自然对数的底；Do即平均致死剂量，它是曲线指数区存活分数下降63%所需的照射剂量，反映不同细胞对射线的敏感性和同一种细胞放射敏感性的变化；N为外推数或靶数，它反映细胞存活曲线肩区大小，N值越大，则细胞在低剂量区时对亚致死损伤的耐受性越大。此外，从细胞存活曲线可测得准阈剂量Dq，它反映肩区大小，表明细胞亚致死损伤修复能力。使用辐射增敏剂后，Dq变小，说明细胞修复亚致死损伤的能力变弱(图6-6)。

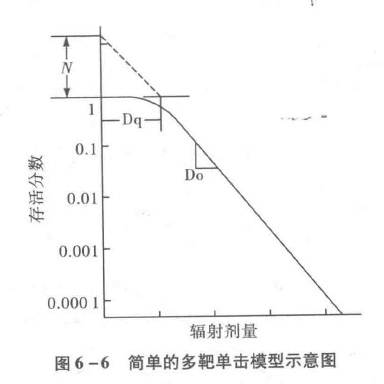
        这个模型假设在细胞死亡前有2个或多个靶受到一次击中。这种曲线的初斜率为0，即认为在低剂量时没有细胞死亡发生。曲线的直线部分为指数性直线，意为细胞存活分数随辐射剂量增加而呈指数性下降。这种模型对受高传能线密度(line-ar energy transfer，LET)辐射的哺乳动物细胞比较合适。

6.5.1.4.2带初斜率的多靶单击模型

        这个模型系在简单的多靶单击模型的方程式上乘上一个带有指数失活特点的校正系数e^-D/Do，得到下列方程：

        S=e^-D/DI[1-(1-e^-D/D2)^N]这条曲线的初始斜率不等于0，也就是说，即使在很低剂量时仍有一些过程能够导致细胞死亡。这个模型实质上是将上述简单多靶单击模型和单击事件综合在一起，是后者造成了非零的初始斜率。这个模型对大多数哺乳动物细胞和较宽能量范围的射线都适用(图6-7)。

6.5.1.4.3线性平方模型

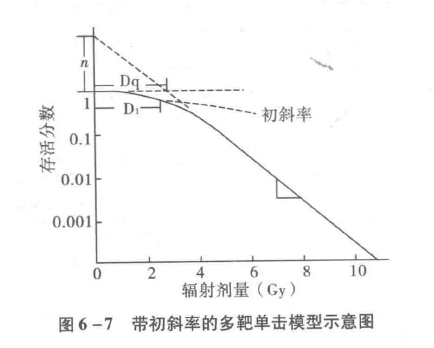
        线性平方模型又称连续弯曲曲线模型，其方程式为：

        S=e^-(αD+ßD2)

        这个模型是以DNA双链断裂时造成细胞死亡的假设建立的。式中n、p分别代表一次冲击和两次冲击所造成DNA双链断裂的参数(图6-8)。